36 Lecture 502
Comparing means

36.1 Libraries

Today’s libraries

mostly working with the usual nycflights13
exposition pipe %$% from the library magrittr

library(tidyverse)
library(magrittr)  
library(nycflights13)

But let’s start from a simple example from datasets

50 flowers from each of 3 species of iris

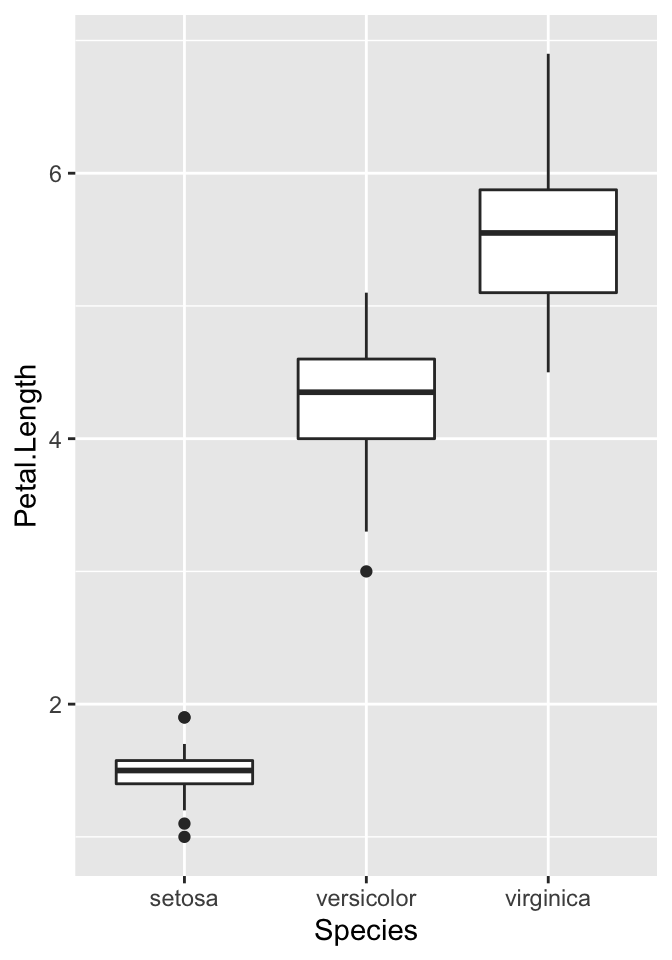
36.2 Example

iris %>% filter(Species == "setosa") %>% pull(Petal.Length) %>% shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.95498, p-value = 0.05481

iris %>% filter(Species == "versicolor") %>% pull(Petal.Length) %>% shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.966, p-value = 0.1585

iris %>% filter(Species == "virginica") %>% pull(Petal.Length) %>% shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.96219, p-value = 0.1098

36.3 T-test

Independent T-test tests whether two group means are different

\[outcome_i = (group\ mean) + error_i \]

groups defined by a predictor, categorical variable
outcome is a continuous variable
assuming
- normally distributed values in groups
- homogeneity of variance of values in groups
  - if groups have different sizes
- independence of groups

36.4 Example

Values are normally distributed, groups have same size, and they are independent (different flowers, check using leveneTest)

iris %>%
  filter(Species %in% c("versicolor", "virginica")) %$% # Note %$%
  t.test(Petal.Length ~ Species)

## 
##  Welch Two Sample t-test
## 
## data:  Petal.Length by Species
## t = -12.604, df = 95.57, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.49549 -1.08851
## sample estimates:
## mean in group versicolor  mean in group virginica 
##                    4.260                    5.552

The difference is significant t(95.57) = -12.6, p < .01

36.5 ANOVA

ANOVA (analysis of variance) tests whether more than two group means are different

\[outcome_i = (group\ mean) + error_i \]

groups defined by a predictor, categorical variable
outcome is a continuous variable
assuming
- normally distributed values in groups
  - especially if groups have different sizes
- homogeneity of variance of values in groups
  - if groups have different sizes
- independence of groups

36.6 Example

Values are normally distributed, groups have same size, they are independent (different flowers, check using leveneTest)

iris %$%
  aov(Petal.Length ~ Species) %>%
  summary()

##              Df Sum Sq Mean Sq F value Pr(>F)    
## Species       2  437.1  218.55    1180 <2e-16 ***
## Residuals   147   27.2    0.19                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The difference is significant t(2, 147) = 1180.16, p < .01

36 Lecture 502Comparing means