37 Lecture 502
Correlation

37.1 Correlation

Two variables can be related in three different ways

• related
  • positively: entities with high values in one tend to have high values in the other
  • negatively: entities with high values in one tend to have low values in the other
• not related at all

Correlation is a standardised measure of covariance

37.2 Example

flights_nov_20 <- nycflights13::flights %>%
  filter(!is.na(dep_delay), !is.na(arr_delay), month == 11, day ==20)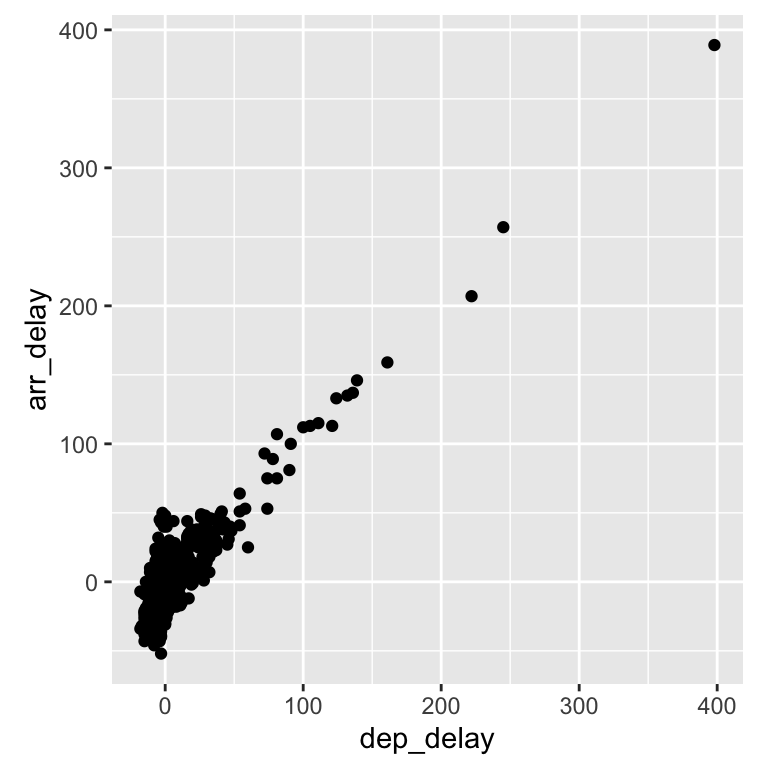 

37.3 Example

flights_nov_20 %>%
  pull(dep_delay) %>% shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.39881, p-value < 2.2e-16

flights_nov_20 %>%
  pull(arr_delay) %>% shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.67201, p-value < 2.2e-16

37.4 Pearson’s r

If two variables are normally distributed, use Pearson’s r

The square of the correlation value indicates the percentage of shared variance

If they were normally distributed, but they are not

• 0.882 ^ 2 = 0.778
• departure and arrival delay would share 77.8% of variance

# note the use of %$%
#instead of %>%
flights_nov_20 %$%
  cor.test(dep_delay, arr_delay)

## 
##  Pearson's product-moment correlation
## 
## data:  dep_delay and arr_delay
## t = 58.282, df = 972, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.8669702 0.8950078
## sample estimates:
##       cor 
## 0.8817655

37.5 Spearman’s rho

If two variables are not normally distributed, use Spearman’s rho

• non-parametric
• based on rank difference

The square of the correlation value indicates the percentage of shared variance

If few ties, but there are

• 0.536 ^ 2 = 0.287
• departure and arrival delay would share 28.7% of variance

flights_nov_20 %$%
  cor.test(
    dep_delay, arr_delay, 
    method = "spearman")

## Warning in cor.test.default(dep_delay, arr_delay, method = "spearman"):
## Cannot compute exact p-value with ties

## 
##  Spearman's rank correlation rho
## 
## data:  dep_delay and arr_delay
## S = 71437522, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.5361247

37.6 Kendall’s tau

If not normally distributed and there is a large number of ties, use Kendall’s tau

• non-parametric
• based on rank difference

The square of the correlation value indicates the percentage of shared variance

Departure and arrival delay seem actually to share

• 0.396 ^ 2 = 0.157
• 15.7% of variance

flights_nov_20 %$%
  cor.test(
    dep_delay, arr_delay, 
    method = "kendall")

## 
##  Kendall's rank correlation tau
## 
## data:  dep_delay and arr_delay
## z = 17.859, p-value < 2.2e-16
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
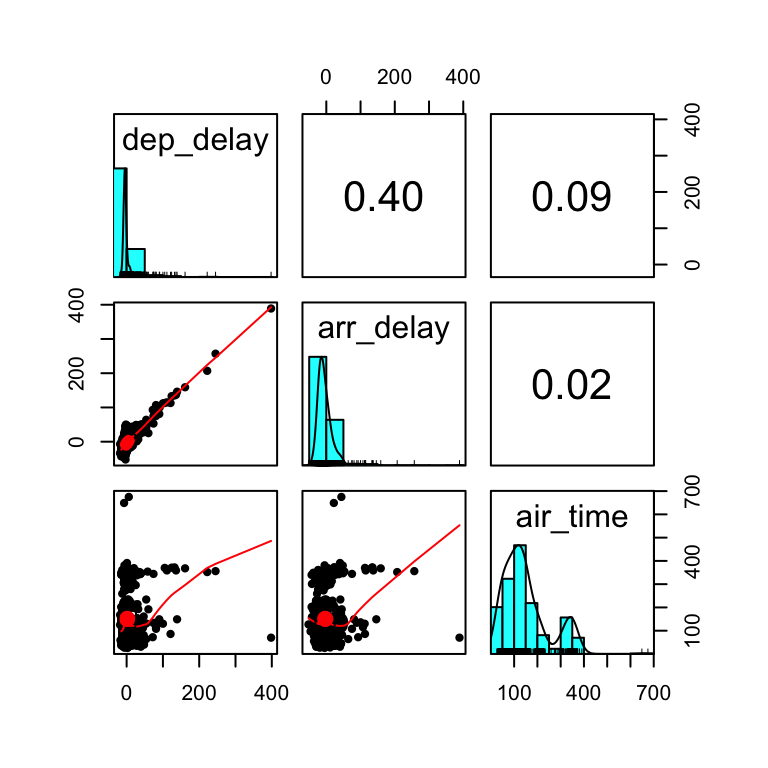
## 0.3956265

37.7 Pairs plot

Combines in one visualisation: histograms, scatter plots, and correlation values for a set of variables

library(psych)

flights_nov_20 %>%
  select(
    dep_delay, 
    arr_delay, 
    air_time
  ) %>%
  pairs.panels(
    method = "kendall"
  )