42 Lecture 601
Clustering

42.1 Clustering task

"Clustering is an unsupervised machine learning task that automatically divides the data into clusters , or groups of similar items". (Lantz, 2019)

Methods:

• Centroid-based
  • k-means
  • fuzzy c-means
• Hierarchical
• Mixed
  • bootstrap aggregating
• Density-based
  • DBSCAN

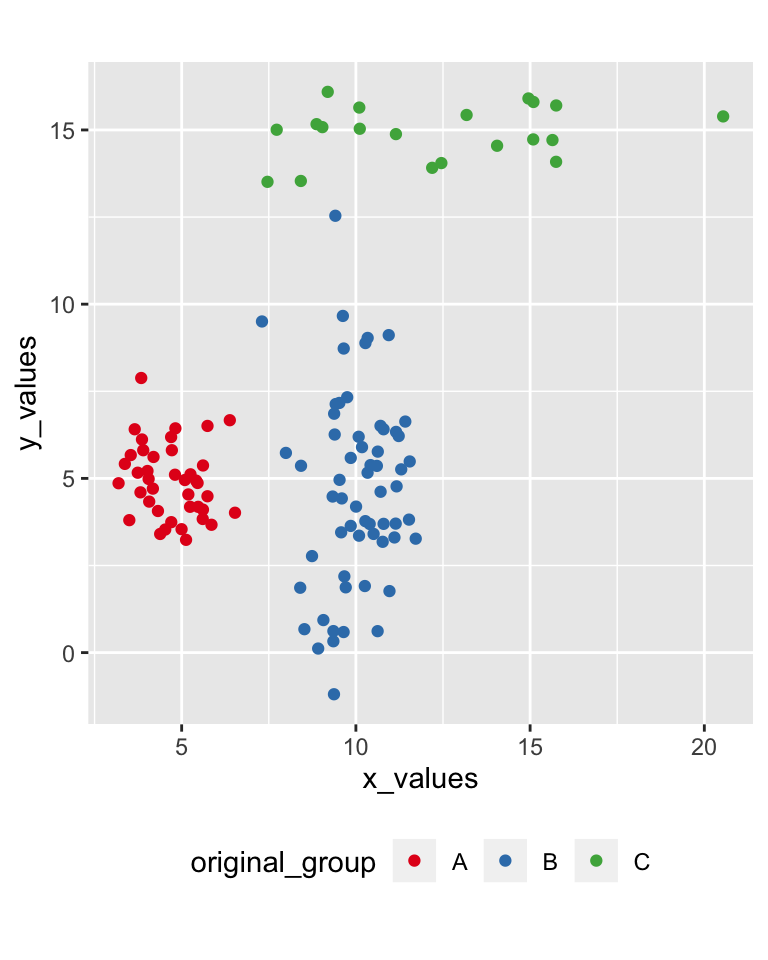
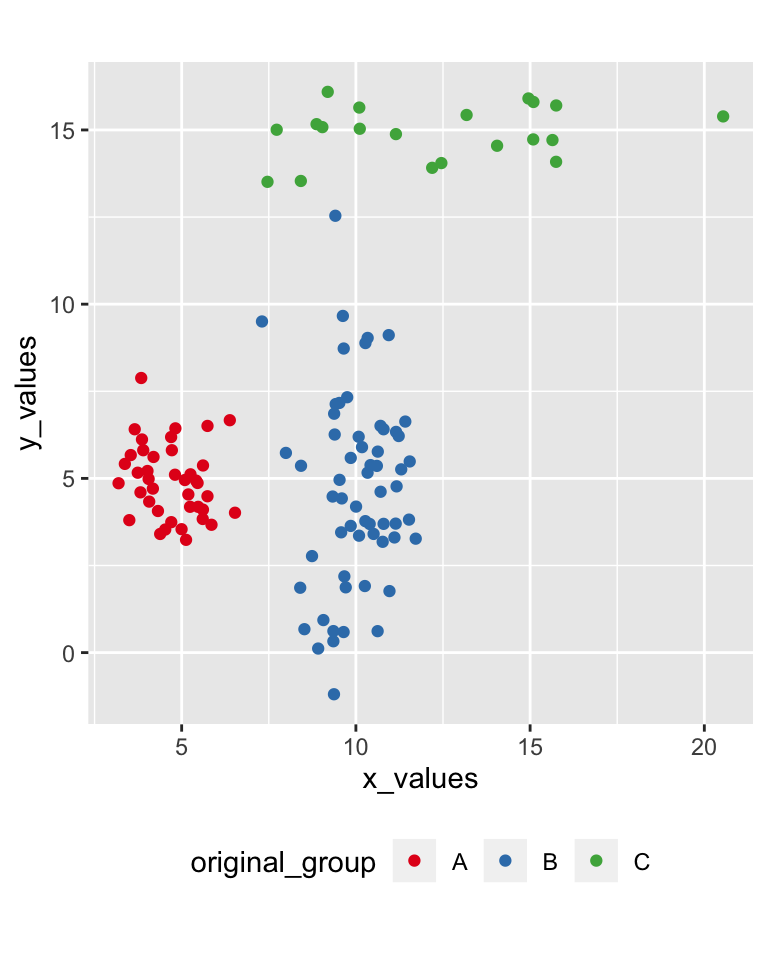
42.2 Example

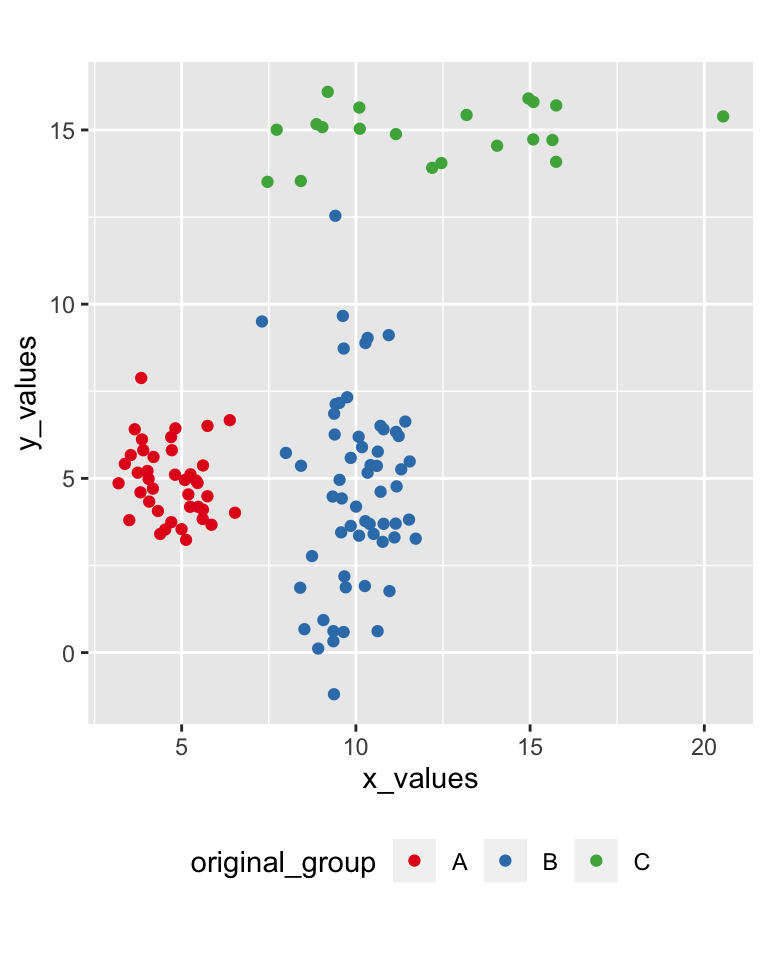
data_to_cluster <- data.frame(
  x_values = c(rnorm(40, 5, 1), rnorm(60, 10, 1), rnorm(20, 12, 3)),
  y_values = c(rnorm(40, 5, 1), rnorm(60, 5, 3), rnorm(20, 15, 1)),
  original_group = c(rep("A", 40), rep("B", 60), rep("C", 20)) )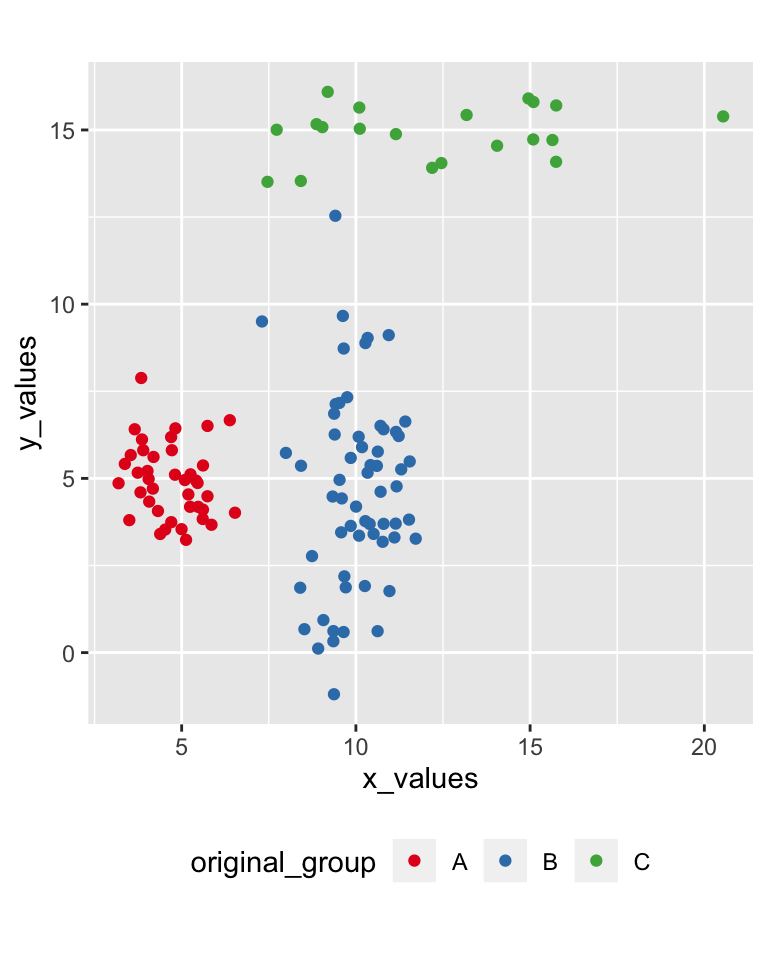

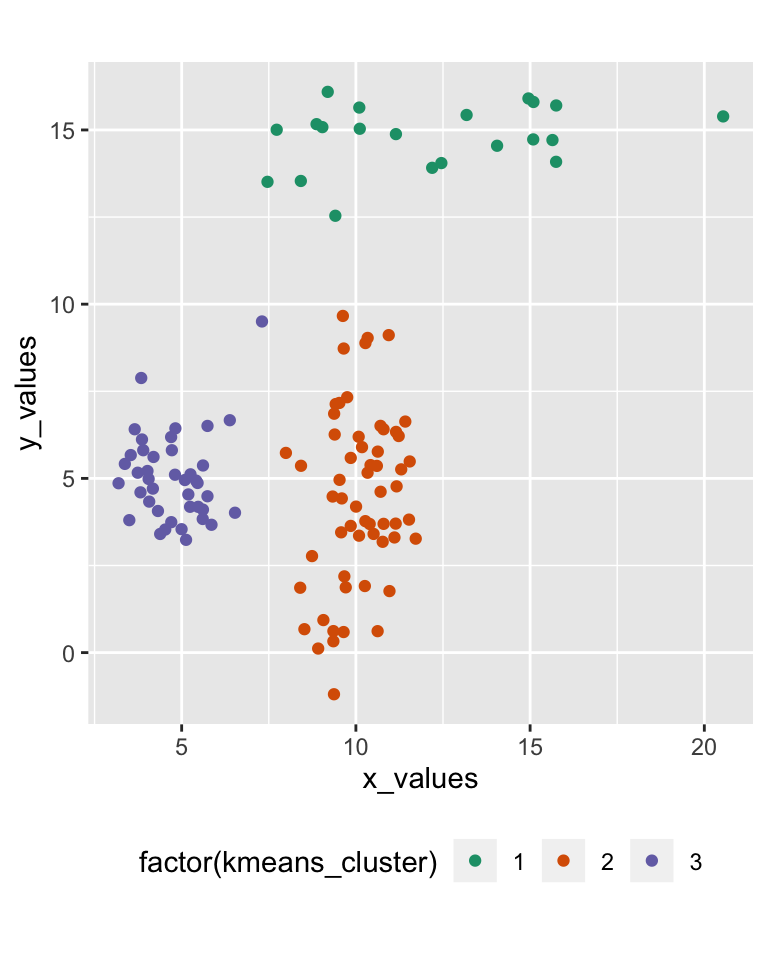
42.3 k-means

k-mean clusters n observations in k clusters, minimising the within-cluster sum of squares (WCSS)

Algorithm: k observations a randomly selected as initial centroids, then repeat

• assignment step: observations are assigned to the closest centroids
• update step: calculate means for each cluster to use as new the centroid

until centroids don’t change anymore, the algorithm has converged

kmeans_found_clusters <- data_to_cluster %>%
  select(x_values, y_values) %>%
  kmeans(centers=3, iter.max=50)

data_to_cluster <- data_to_cluster %>%
  add_column(kmeans_cluster = kmeans_found_clusters$cluster)

42.4 K-means result

42.5 Fuzzy c-means

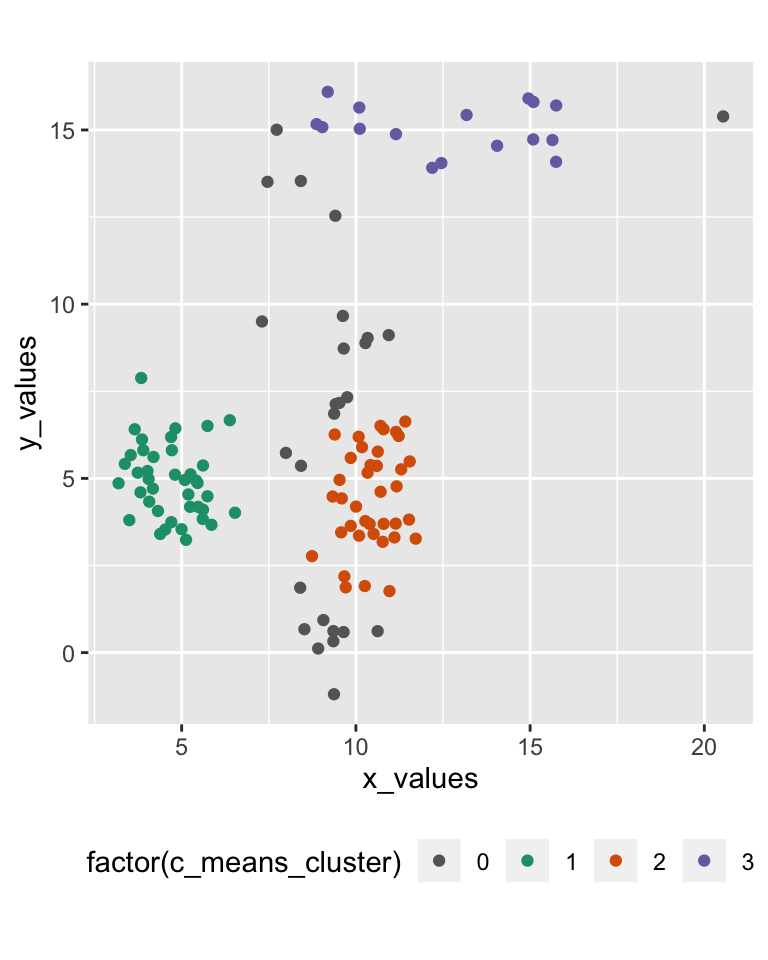
Fuzzy c-means is similar to k-means but allows for "fuzzy" membership to clusters

Each observation is assigned with a value per each cluster

• usually from 0 to 1
• indicates how well the observation fits within the cluster
• i.e., based on the distance from the centroid

library(e1071)

cmeans_result <- data_to_cluster %>%
  select(x_values, y_values) %>%
  cmeans(centers=3, iter.max=50)

data_to_cluster <- data_to_cluster %>%
  add_column(c_means_assigned_cluster = cmeans_result$cluster)

42.6 Fuzzy c-means

A “crisp” classification can be created by picking the highest membership value.

• that also allows to set a membership threshold (e.g., 0.75)
• leaving some observations without a cluster

data_to_cluster <- data_to_cluster %>%
  add_column(
    c_means_membership = apply(cmeans_result$membership, 1, max)
  ) %>%
  mutate(
    c_means_cluster = ifelse(
      c_means_membership > 0.75, 
      c_means_assigned_cluster, 
      0
    )
  )

42.7 Fuzzy c-means result

42.8 Hierarchical clustering

Algorithm: each object is initialised as, then repeat

• join the two most similar clusters based on a distance-based metric
• e.g., Ward’s (1963) approach is based on variance

until only one single cluster is achieved

hclust_result <- data_to_cluster %>%
  select(x_values, y_values) %>%
  dist(method="euclidean") %>%
  hclust(method="ward.D2")

data_to_cluster <- data_to_cluster %>%
  add_column(hclust_cluster = cutree(hclust_result, k=3))

42.9 Clustering tree

This approach generates a clustering tree (dendrogram), which can then be “cut” at the desired height

plot(hclust_result) + abline(h = 30, col = "red")

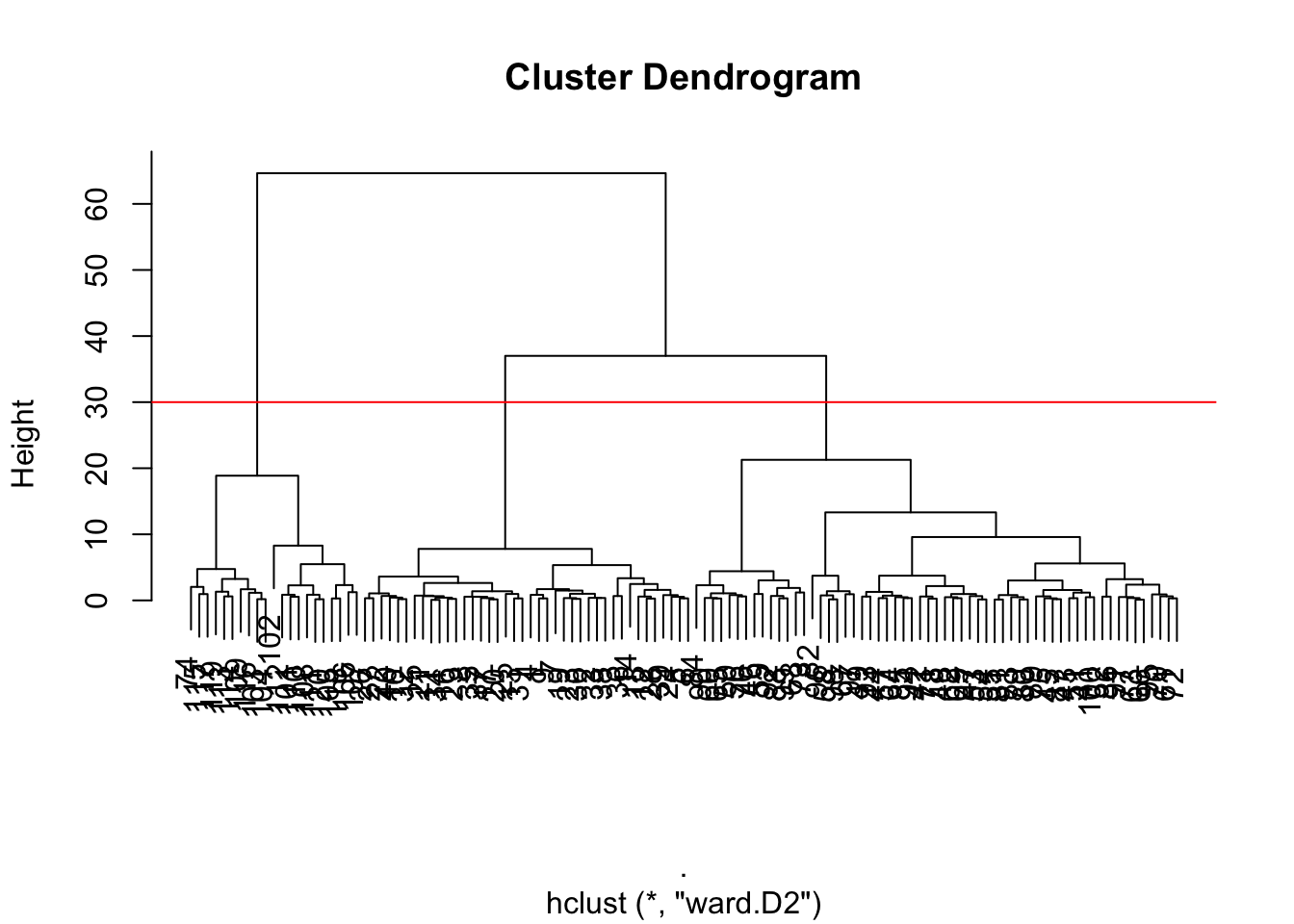
## integer(0)

42.10 Hierarchical clustering result

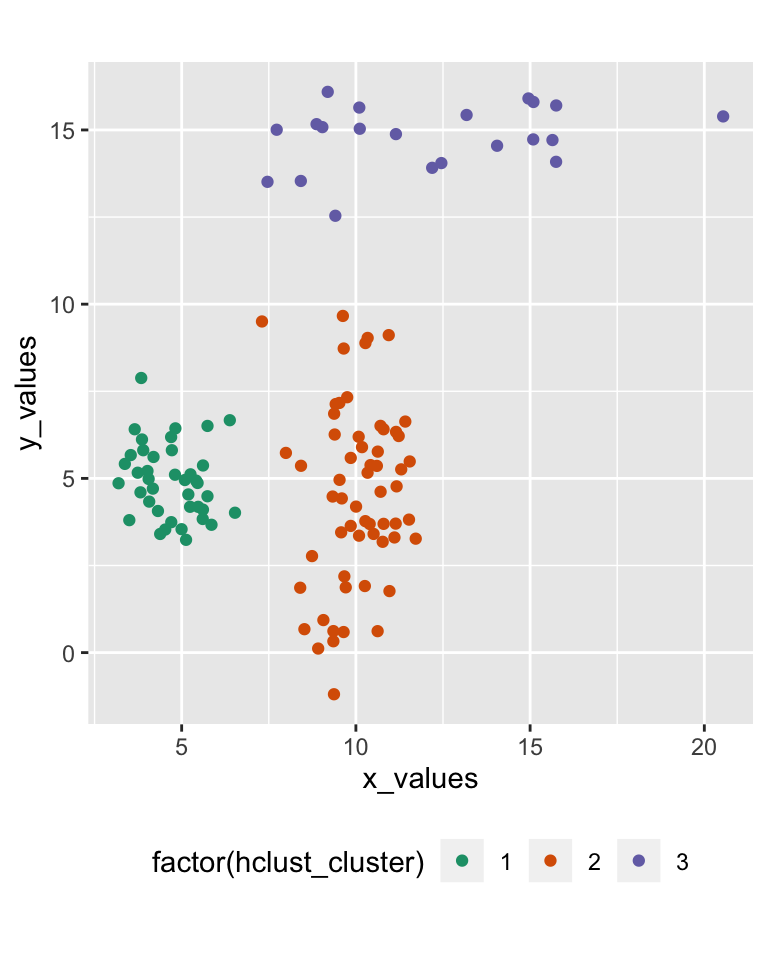
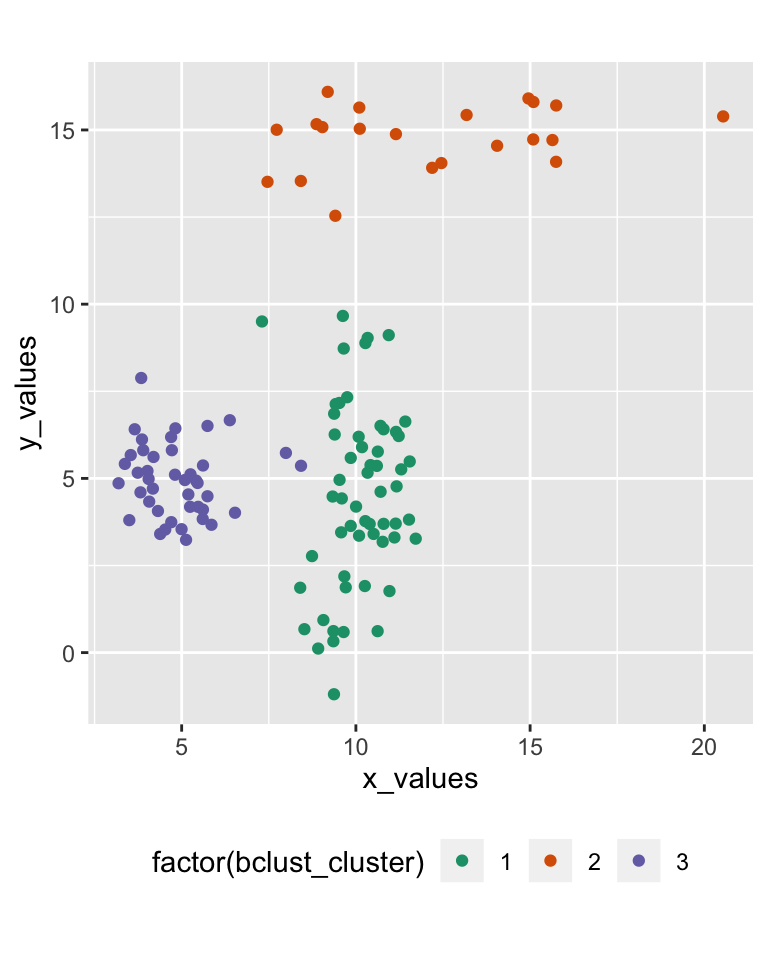
42.11 Bagged clustering

Bootstrap aggregating (b-agg-ed) clustering approach (Leisch, 1999)

• first k-means on samples
• then a hierarchical clustering of the centroids generated through the samples

library(e1071)

bclust_result <- data_to_cluster %>%
  select(x_values, y_values) %>%
  bclust(hclust.method="ward.D2", resample = TRUE)

data_to_cluster <- data_to_cluster %>%
  add_column(bclust_cluster = clusters.bclust(bclust_result, 3))

42.12 Bagged clustering result

42.13 Density based clustering

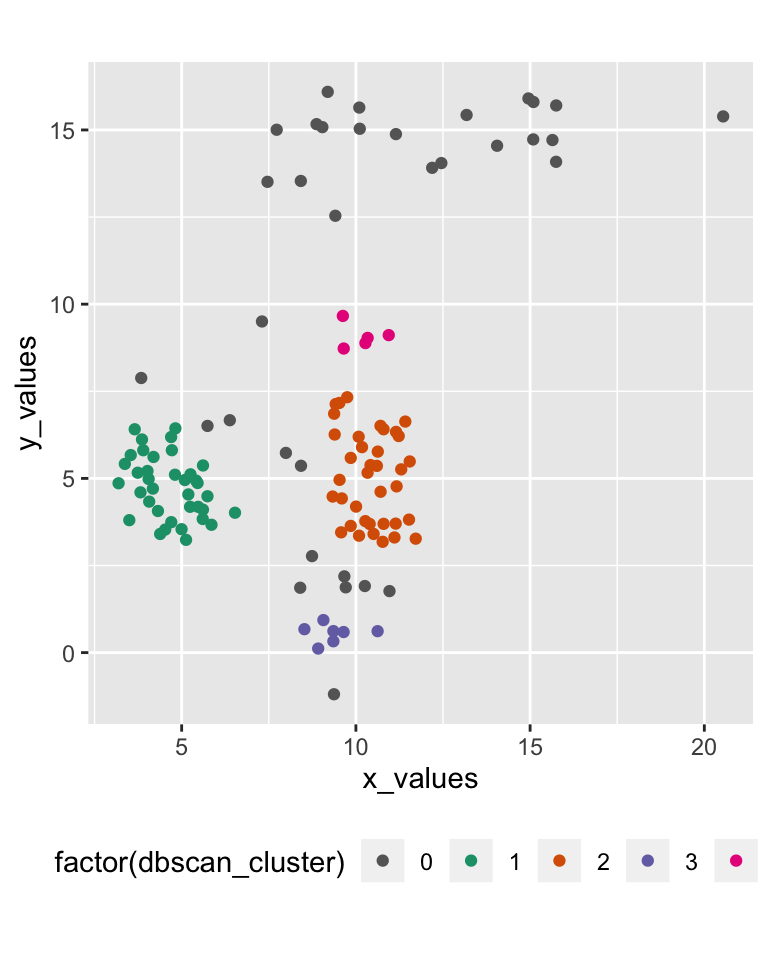
DBSCAN (“density-based spatial clustering of applications with noise”) starts from an unclustered point and proceeds by aggregating its neighbours to the same cluster, as long as they are within a certain distance. (Ester et al, 1996)

library(dbscan)

dbscan_result <- data_to_cluster %>%
  select(x_values, y_values) %>%
   dbscan(eps = 1, minPts = 5)

data_to_cluster <- data_to_cluster %>%
  add_column(dbscan_cluster = dbscan_result$cluster)

42.14 DBSCAN result

42.15 Geodemographic classifications

In GIScience, the clustering is commonly used to create geodemographic classifications such as the 2011 Output Area Classification (Gale et al., 2016)

• initial set of 167 prospective variables from the United Kingdom Census 2011
  • 86 were removed,
  • 41 were retained as they are
  • 40 were combined
  • final set of 60 variables.
• k-means clustering approach to create
  • 8 supergroups
  • 26 groups
  • 76 subgroups.